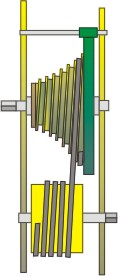
fig. 1 |
La
molla di carica di un orologio, svolgendosi, conferisce energia
al sistema. Peraltro detta quantità di energia varia
con il variare dello stato di carica della molla. E del
nefasto effetto che questa variazione comporta alla qualità
dell'oscillazione del pendolo, oramai, siamo ben consci.
La differenza tra la quantità di energia conferita dalla
molla al pendolo tramite lo scappamento quando essa è completamente
carica e quando è scarica, è la maggiore
responsabile dell'errore circolare e quindi è
molto importante cercare di rendere uniforme l'"output"
della quantità di energia della molla di carica al fine
di evitare l'insorgere di errori.
Una soluzione al problema è data dall'utilizzo del conoide.
Come si può vedere dalla figura, l'energia della molla
non viene conferita direttamente al treno degli ingranaggi ma
tramite il conoide.
Quando la molla è completamente carica la catena è
impegnata nella estremità più rastremata del conoide
ed il momento torcente che si genera ( forza:"tanta"-braccio:corto)
sarà "eguale" a quando la molla sarà scarica
e la catena è impegnata nella parte "grande"
del conoide ( forza:"poca"- braccio:"lungo")
|
|
Naturalmente
perchè si verifichi questa "eguaglianza"
sia alle due estremità che durante tutto lo svolgimento
della catena dal conoide ,ed anche tenendo conto che la
quantità di energia liberata dalla molla di carica
non ha un andamento costante, esso deve avere una sagoma
appropriata.
La
curvatura del conoide quindi dovrà rispettare una
complessa formula matematica che tiene conto di tutte le
variabili citate.
|
|
Ovvero
:
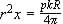
dove
r
= raggio variabile del conoide
x = distanza dalla parte posteriore del
conoide
p = passo delle scanalature
R = raggio del bariletto
k = costante
|
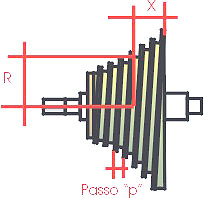 |
per stabilire la costante k si assegna un valore
al raggio r per l'estremità più
piccola del conoide e si fanno i relativi calcoli .
Io, per definire detta curva adopero la molto più pratica
"regola del pollice".Essa consiste
nel traguardare la forma del mio dito pollice con quella del costruendo
conoide. Per quanto mi riguarda, quando esse coincidono, sono
soddisfattissimo ... E sfido qualunque matematico a dimostrarmi
che il profilo del mio conoide non è adeguatamente funzionale.....
|